浮点数计算和比较的坑 今天有一个小伙伴给我发来了一个截图如下。我下意识的说了一句:0.58*50 不等于 29。 感概,有时候,眼见也不一定为实。这就是一个浮点运算导致的「算不准」问题。 在历史上,其实已经有过类似因为浮点运算导致的事故。 1994 年,英特尔的奔腾微处理器芯片的浮点计算单元出现了一个 Bug。在某些情况下,浮点除法并不能返回正确的结果。例如 4195835.0/3145727.0 产生的是 1.33374 而不是 1.33382。虽然这个 Bug 可能对绝大多数人没有影响,但是市面上 500 万左右流通的芯片都存在该缺陷,随着整个事件的发酵,最终这个 Bug 给 intel 造成了 4.75 亿美元的损失。这次事件也被称为「Pentium FDIV bug」而载入了 Bug 史册。 我们分别在 R 中计算 0.58*50,0.29*100,然后让他们和 29 互相比一比。 结果如下所示: 我们看到屏幕上显示的 a , b 和 c 都是 29,但是如果用 浮点数的精度和计算问题,在任何编程语言里都类似。 浮点数在计算机中不能以任意精读存储,都会有一个准确性的限制,通过有限的连续字符来保存浮点数。 目前常见的浮点格式包括:单精度,双精度和扩展双精度。他们的准确性从前到后依次提高,其中单精度可以用于一般计算,双精度用于科学计算。在 R 中就是采用了双精度来对浮点数进行保存。如下所示: 我们让 d 等于 10,通过 这里又涉及到了存储模式和类型的问题。在 R 中 继续回来说浮点数的比较。因为精度问题,在 R 语言中使用 就像文章开头的例子,此时假设你有一个 if 语句,想进行一下结果的判断。如果判断条件是 0.29*100 == 29,就会返回 F。因为 0.29*100 的实际值在计算机中比 29 要小一些。当你使用 这也就是为什么 如何解决这个问题呢?在 R 语言中有一个函数叫做 这让我不禁想到了一款果子和洲更(当然还有我)都在用全面屏 Almost 手机。 你可能会问,这个一丢丢究竟是多少呢? 通过帮助文档,我们可以发现这个一丢丢实际是 这里的 回到最开始的问题,如果确实需要 在 R 中有 3 种常见的取整,分别是: 此外还有一种不常用的「向 0 看齐」取整方法 他们的差别如下: 因此通过 写到这里并没有结束,因为如果用 python 算一下,就会发现 0.58*100 真的不等于 58。感觉 R 语言的对于浮点运算结果的展示还是有点问题?同时,0.58 和 0.59 还是不一样。 看来,要知其所以然,还得再仔细学习一下浮点精度和计算的实质。 参考资料: 本文作者:思考问题的熊 版权声明:本博客所有文章除特别声明外,均采用 知识共享署名-非商业性使用-禁止演绎 4.0 国际许可协议 (CC BY-NC-ND 4.0) 进行许可。 如果你对这篇文章感兴趣,欢迎通过邮箱订阅我的 「熊言熊语」会员通讯,我将第一时间与你分享肿瘤生物医药领域最新行业研究进展和我的所思所学所想,点此链接即可进行免费订阅。29 怎么会不等于 29
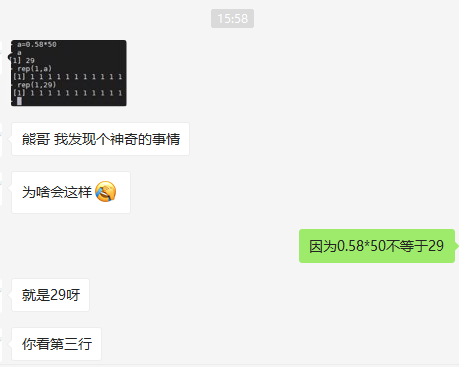

R 语言中的实际示例
(a=29)
(b=0.58*50)
(c=0.29*100)
a==c
a==b
b==c
> (a=29)
[1] 29
> (b=0.58*50)
[1] 29
> (c=0.29*100)
[1] 29
> a==c
[1] FALSE
> b==c
[1] TRUE
> a==b
[1] FALSE
==进行一下比较,发现0.58*50和0.29*100竟然都不等于 29。嗯,很迷。> (d <- 10)
[1] 10
> class(d)
[1] "numeric"
> typeof(d)
[1] "double"
class 可以看出它是一个数值型变量,如果用 typeof 查看,就会发现他的存储模式(storage mode)是一个双精度浮点型数字。class返回的是一个对象的高级类,而typeof返回的是对象的内部低级类。如果用calss查看一个数据框,其返回结果就是他的类(calss)为数据框,如果使用typeof查看,返回的结果就是内部类型为列表,如下所示。(嗯,想起了果子老师课上讲的,data.frame 就是一种特殊的 list)> class(iris)
[1] "data.frame"
> typeof(iris)
[1] "list"
== 进行浮点数的比较是非常危险的。as.interger去处理的时候,结果为 28。> as.integer(0.29*100)
[1] 28
rep(1,29)有 29 个数字,但是rep(1,0.29*100)有 28 个数字。如何避免浮点数计算的坑
all.equal,虽然名字是 equal,但是他其实是 almost equal。
all.equal() 的功能是 Test If Two Objects Are (Nearly) Equal。也就是它可以略微忍受两个对象之间有一丢丢差别。如下所示:> (a=29)
[1] 29
> (b=0.58*50)
[1] 29
> (c=0.29*100)
[1] 29
> a==b
[1] FALSE
> all.equal(a,b)
[1] TRUE
> a==c
[1] FALSE
> all.equal(a,c)
[1] TRUE
tolerance = sqrt(.Machine$double.eps)。如果实际运行一下会发现.Machine$double.eps 等于 2.220446e-16,那么sqrt(.Machine$double.eps)就是 1.490116e-08。.Machine是一个存储了 R 正在运行机器的数值特性的变量,其中包括了最小正浮点数(double.eps)。因此,以后想进行类似的比较,记得使用all.equal()。另外,多说一句,在 if 判断中不要直接使用它,而是写成 isTRUE(all.equal(....)) 。rep(1,rep(1,0.29*100))返回 29 个数字,就可能需要用到取整。
floor()ceiling()round()trunc()。> ( x1 <- seq(-2, 4, by = .5) )
[1] -2.0 -1.5 -1.0 -0.5 0.0 0.5 1.0 1.5 2.0 2.5 3.0 3.5 4.0
> floor(x1)
[1] -2 -2 -1 -1 0 0 1 1 2 2 3 3 4
> ceiling(x1)
[1] -2 -1 -1 0 0 1 1 2 2 3 3 4 4
> round(x1)
[1] -2 -2 -1 0 0 0 1 2 2 2 3 4 4
> trunc(x1)
[1] -2 -1 -1 0 0 0 1 1 2 2 3 3 4
rep(1,round(0.58*50))就可以得到和rep(1,29)一致的结果了。>>> 0.58*100
57.99999999999999
>>> 0.59*100
59.0
>>> 0.57*100
56.99999999999999
>>> 0.56*100
56.00000000000001
R FAQ 7.31
· 分享链接 https://kaopubear.top/blog/2019-12-19-rfloat/