思考问题的熊
很高兴和你相遇
这里正在记录我的所思所学
订阅免费邮件通讯接收最新内容
首页 归档 想法 通讯 播客 工具 简历 关于

统计学基础与 R-8

2017-10-03, 2331 words, 9 min read

写在前面

入门生物信息，所有人都绕不开统计基础知识和相关实现方式。本章我们将简要介绍统计学相关基础知识以及如何使用 R 语言进行简单地计算和分析

第八节 常用高阶分析方法

回归分析

所谓回归分析 (regression analysis)，在统计学中有着非常重要的作用，从大的层面来讲指用自变量（解释变量或者预测变量）来预测因变量（相应变量或者结果变量）的方法。比如在几个自变量中找到和因变量更相关的一个，利用自变量和因变量的关系生成等式对因变量进行预测。从小的层面来说，回归的模型非常之多，也非常复杂，例如最小二乘回归，logistic 回归和泊松回归等等。

最小二乘回归是最常用到的回归模型，包括简单线性回归（一元一阶），多项式回归（一元多阶）和多元线性回归（多元）。所谓最小二乘法是用一条直线y=ax+by=ax+b（回归线）拟合一组两变量数据的方法，使得误差平方和（点到直线的距离平方和）最小。对数据进行最小二乘回归分析时，要求数据符合正态分布，独立和同方差性。

简单线性回归可以使用 F 检验，拟合优度 (R2R^2) 为回归平方和/总平方和，代表因变量可以被自变量解释的比例。

相关系数 (r) 描述个数据点与直线的偏离程度，度量回归线和数据的拟合程度。

在 R 中，lm()是拟合回归模型最简单的函数。针对两个变量，我们一般会先通过简单线性回归进行拟合，通过结果图，根据具体的需要再增加二次项提高预测精度。类似之前提到的 ANOVA 分析，可以使用summary()函数获取回归模型的详细参数和统计量。

有的时候，我们希望能够让回归模型尽量的简单，既减少自变量的数量还不影响对因变量预测的准确对。这是就可以使用anova()函数，查看是否可以删掉一些回归系数不显著的变量。

如果因变量不符合正态分布或者非连续变量，我们就需要考虑使用广义线性模型来进行拟合。当因变量为类别性变量（二项分布）时可以使用 logistic 回归，当因变量为计数型（泊松分布）可以使用泊松回归。在 R 中，这两种方法都可以使用 glm() 来进行计算。

聚类分析

聚类分析是统计中另一个非常重要的方法，可以帮助我们在多维度的数据中把相似的数据归为子集，每个子集中的数据都具有某种程度的相似性。在具体的生物研究中，聚类可以帮助我们通过表达类似的基因找到功能相关的基因，或者帮助推测未知基因的功能。通常聚类分析也被称作非监督机器学习。

进行聚类分析首先需要计算不同观测值之间的距离，进而生成聚类使用的距离矩阵。
计算距离的方法有很多，选择不同的距离计算方法也会对最终的聚类结果产生很大的影响。常用的距离计算方法有欧氏距离 (Euclidean distance)、曼哈顿距离 (Manhattan distance) 和基于相关性距离 (correlation-based distances) 的 Pearson correlation distances、Spearman's rank correlation、Kendall correlation distance 等等。

另外，在构建距离矩阵之前，往往会对原始的观测数据进行标准化，如计算 z score。

总的来说，聚类方法从整体上主要使用的有 Partitioning method 和 Hierarchical Clustering 两类，其中 Partitioning 包括 K-means clustering，K-medoids clustering(PAM) 等具体方法。

k-means

在 k-means 算法中，首先我们需要确定数据最终分为几类 (k)，然后会根据分类数量随机选取 k 个点最为每个类的初始质心（这也是同一组数据每次聚类的结果都不尽相同的原因），随后其他的点都会通过欧式距离找到分到和自己最近的初始中心。通过一次这样的过程之后，再根据每个集合中的点计算均值得到新的质心，重复之前的过程进行迭代。每次迭代，每个集合中的质心都会重新产生，所有的非质心点再重新分配给新的质心形成集合。如果在一次迭代中，只有非常少的点会发生集合的转移则迭代停止。

需要注意的是，k-means 聚类的方法对异常值非常敏感，与之相比 PAM 要好一些。

在 R 中，kmeans 聚类可以使用 stats 包中的kmeans()函数，如果想使用 K-medoids clustering 可以借助 cluster 包中的pam()函数。另外，在进行 cluster 和 pca 相关的分析中，factoextra 也是一个不错的选择，包括了各种常用的功能。

一个比较完整的 k-means 聚类分析过程主要包括数据标准化，评估合适 cluster 数数目，进行计算以及可视化展示等步骤。

Hierarchical Clustering

层次聚类和 k-means 相比不需要预先设定聚类的数目，最终的聚类结果会以颠倒树状结构显示，不同类别观测值在树的最底层（树叶），越向上节点越少。层次聚类可以细分为 Agglomerative Clustering 和 Divisive Hierarchical，前者的思路是从“树叶”向“树干”聚集，后者的思路是从“树干”向“树叶”分裂。一般而言，Agglomerative Clustering 适合在 clusters 比较少时使用；而 Divisive Hierarchical 适合在有大量 clusters 时使用，可以选择到那一步停下不再细分。

以 Agglomerative Clustering 为例，大致流程是首先将每个对象归为一类，每类仅包含一个对象，计算类与类之间的距离。找到最近的两个类然后合并，接着计算新类与所有旧类之间的距离。重复之前的过程，直到最后合并成一个类为止。

根据类间距离计算方法的不同，又可以分为五种：single-linkage（类和类两组对象间的最小距离）、 complete-linkage（类和类两组对象间的最大距离）、 average-linkage（两组对象间的平均距离）、centroid linkage 和 Ward′s method（在每一步使组内离差平方和增量最小）。

一个比较完整的层次聚类分析过程主要包括数据标准化，计算距离，构建聚类树，确定分组以及可视化展示等步骤。

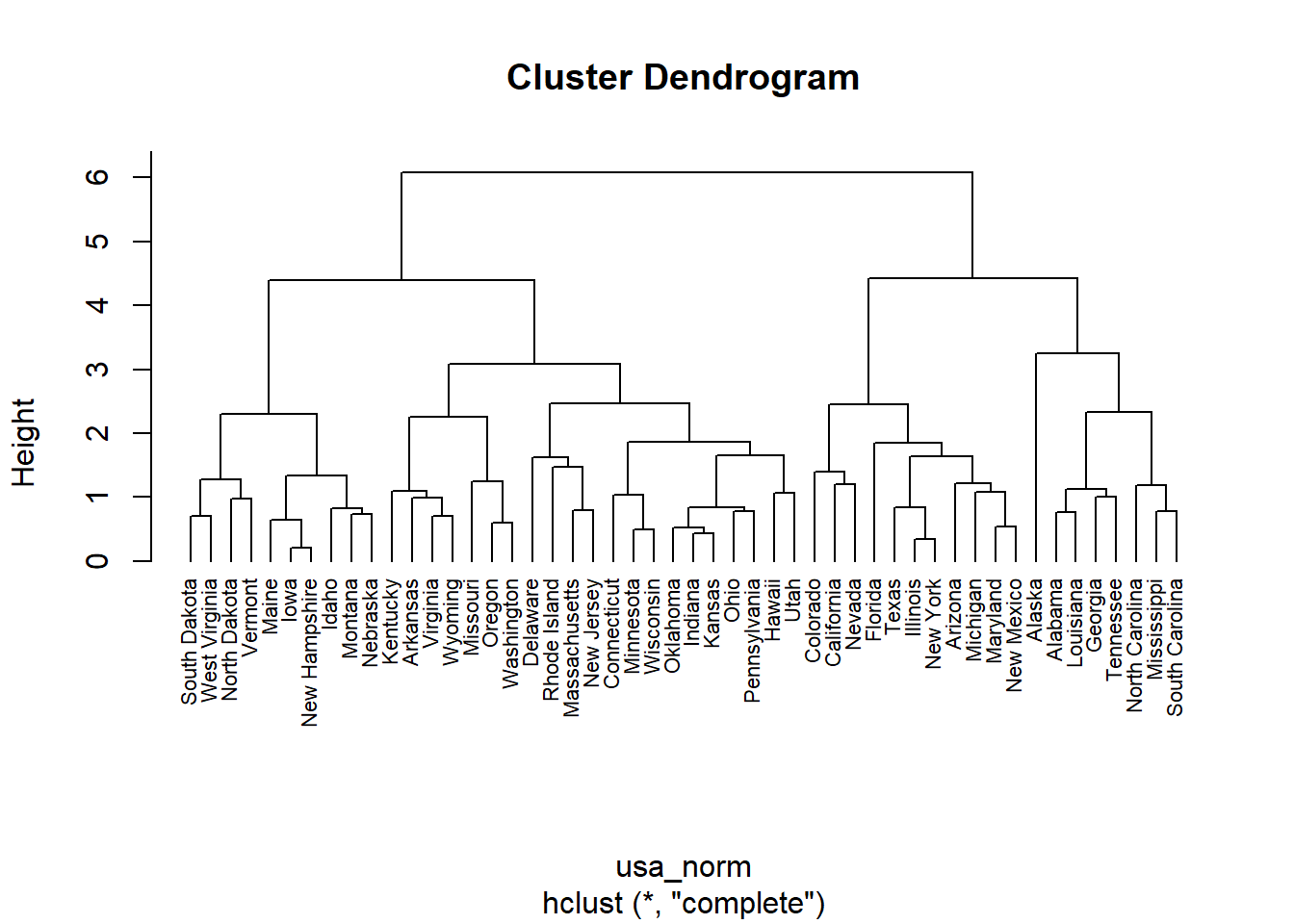
在 R 中，计算距离时可以使用dist()函数，构建聚类树可以使用hclust()函数，将树分组可以使用cutree()。当然也可以使用 cluster 包同时完成上面几个步骤。

以 R 中数据集 USArrests 为例，进行聚类分析。

# 标准化
usa_norm <- dist(scale(USArrests), method = "euclidean")

# 构建树
hc <- hclust(usa_norm, method = "complete")

# install.packages(c("factoextra", "dendextend"))
# 可视化展示
library(factoextra)
#基础
plot(hc, hang = -1, cex = 0.7)

#美化
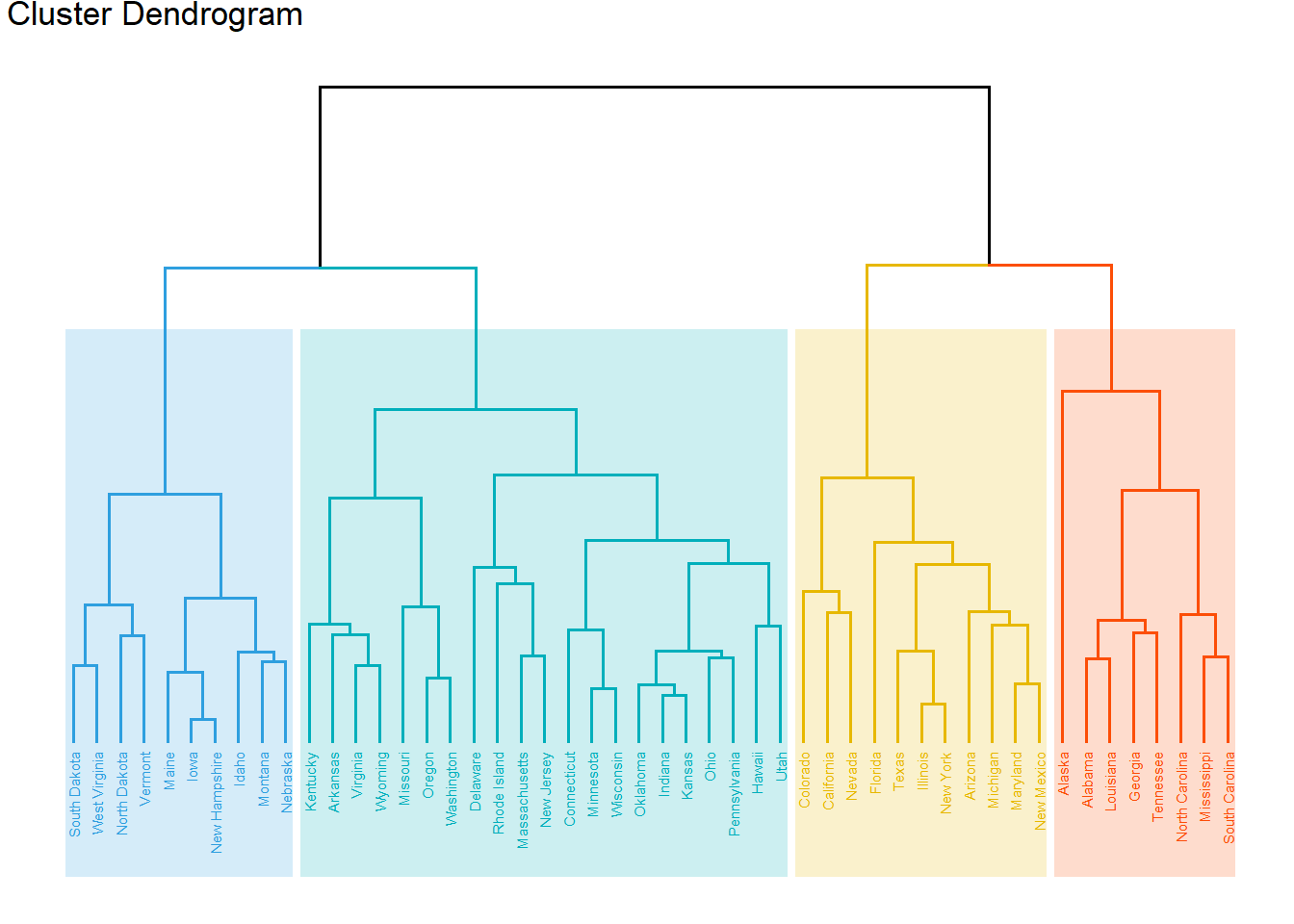
fviz_dend(hc, k = 4,      # 分为 4 类
          cex = 0.4,      # label 大小，防止字不显示完全
          k_colors = c("#2E9FDF", "#00AFBB", "#E7B800", "#FC4E07"),
          color_labels_by_k = TRUE,  # color labels by groups
          rect = TRUE, # Add rectangle around groups
          rect_fill = TRUE,
          rect_border = c("#2E9FDF", "#00AFBB", "#E7B800", "#FC4E07"),
          ggtheme = theme_void() # ggplot2 主题
          )

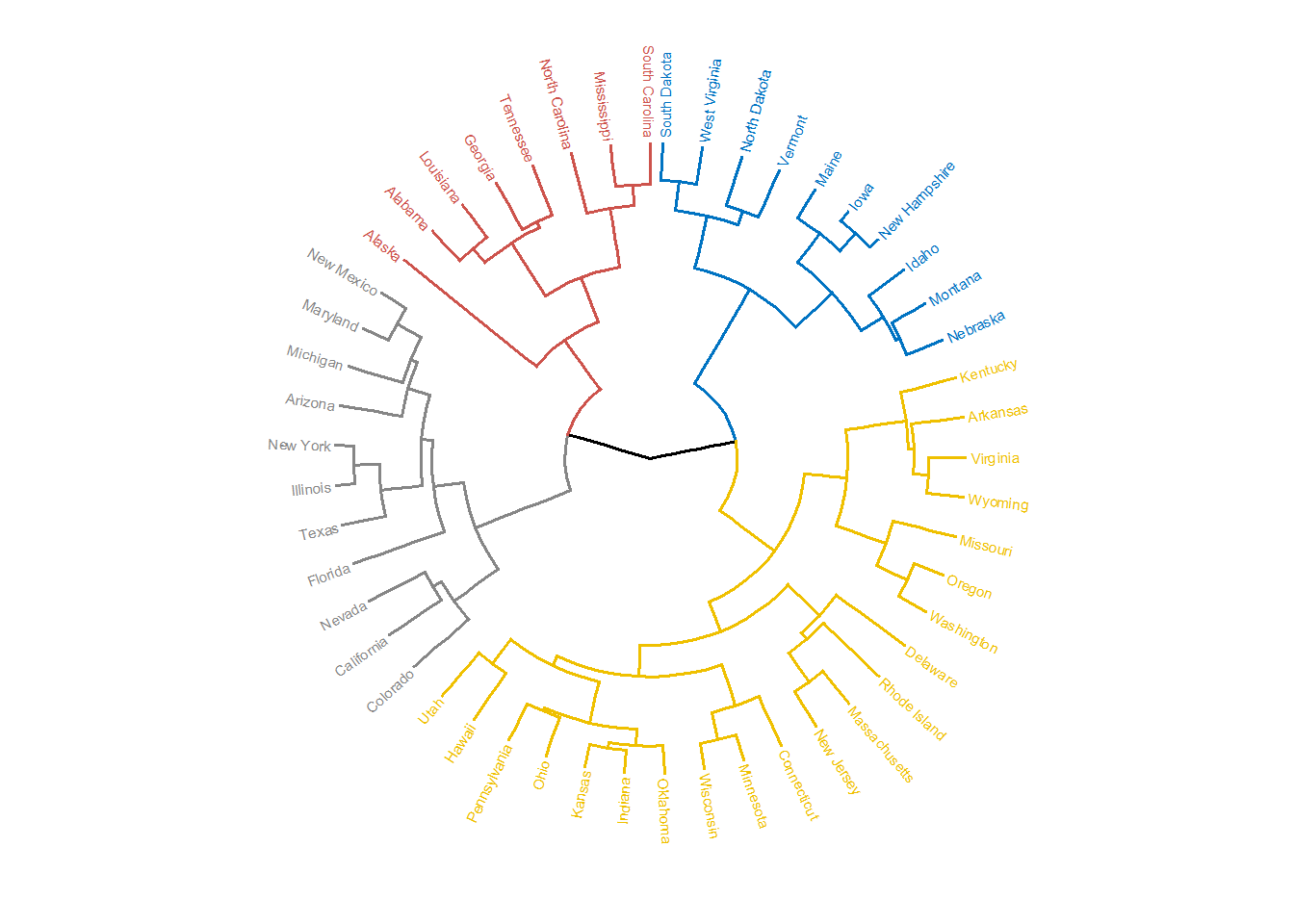
# 环形
fviz_dend(hc, cex = 0.4, k = 4,
          k_colors = "jco", type = "circular")

主成分分析

当数据集中变量过多时，会为我们的分析带来很大的不便，在这些变量中很可能存在冗余成分。为了减少冗余变量，降低数据维度，只留下少数能够依旧很好预测因变量的不相关变量，我们可以使用主成分分析 (PCA) 方法。

在 R 中，内置函数procomp()可以用来进行 PCA 分析，以 R 中数据集 iris 为例

# 只支持数值型变量，所以提取原数据集前 4 列
ir_num <- iris[, 1:4]

# 进行 pca 分析
ir_pca <- prcomp(ir_num,
                 scale. = TRUE)
# 查看主成分信息
summary(ir_pca)

# Importance of components%s:
#                           PC1    PC2     PC3     PC4
# Standard deviation     1.7084 0.9560 0.38309 0.14393
# Proportion of Variance 0.7296 0.2285 0.03669 0.00518
# Cumulative Proportion  0.7296 0.9581 0.99482 1.00000

通过上述结果可以发现，主成分 1 和 2 可以解释 0.95 的变化。

本文作者：思考问题的熊

版权声明：本博客所有文章除特别声明外，均采用 知识共享署名-非商业性使用-禁止演绎 4.0 国际许可协议 (CC BY-NC-ND 4.0) 进行许可。

如果你对这篇文章感兴趣，欢迎通过邮箱或者微信订阅我的 「熊言熊语」会员通讯，我将第一时间与你分享肿瘤生物医药领域最新行业研究进展和我的所思所学所想，点此链接即可进行免费订阅。


· 分享链接 https://kaopubear.top/blog/2017-10-03-RandStatistics8/

R 数据科学 统计
Powered byGridea&Theme OnePlus
△