入门生物信息,所有人都绕不开统计基础知识和相关实现方式。本章我们将简要介绍统计学相关基础知识以及如何使用 R 语言进行简单地计算和分析。 在上一节讨论了单样本和双样本均值比较的几种情况,但是很多实验不仅仅有两组样本。进行多组样本之间的均值比较就需要进行单因素方差分析 (one-way analysis of variancd) 和双因素方差分析 (two-way analysis of variancd) 在单因素方差分析模型中样本的组数是任意的但是要求样本之间相互独立,每一组的观测值符合正态分布的同时方差相等,目的是比较每个组的均值。原假设是各组间均值相等(观察的差异有随机误差构成),备择假设是至少有一组和其他组均值不同。数据的变异通常来自于组内部的变异和组间真是变异,其中组内变异一方面由个体差异导致,一方面由实验误差导致,而组间变异则是由不同的处理(因子)导致。如果通过计算,非系统性的变异(组内误差)远大于由不同处理造成的变异(组间变异)如下图 b 所示,则接受原假设,反之则拒绝原假设,如下图 a 所示。 其中组间平均平方和=组间 MS=BetweenSS/(k-1),k-1 为组间自由度,组内平局平方和=组内 MS=WithinSS/(n-k),n-k 为组内自由度,显著性检验建立在组间平均平方和与组内平均平方和的比值上,且该比值为 F 分布,自由度为 k-1, n-k。 具体到 R 中,使用 R 中的 PlantGrowth 数据集举例。该数据有两个实验组和一个对照组,数据的整体情况上文已经统计过,下面通过 box plot 进行形象化展示(使用前文提到过的 ggpubr 包)。 检测正态分布和方差齐性 不符合前提条件时 如果此步骤检测方差不齐性,可以使用** Welch’s ANOVA**, 如果不符合正态分布模型,可以使用非参数检验** Kruskal-Wallis test**, 进行 one-way ANOVA 分析 通过 aov(),我们只能判断这三组数据之间均值不相等,但是不知道具体哪组存在差别。为了知道具体的差异情况,可以采用如下三种方法。 当进行任意两组间比较时,需要考虑由 family-wise error rate 造成的 p 值误差,需要对 p 值进行校正以保证任何两组之间显著性差异的总体概率可以维持在一个固定的显著性水平。常用的校正方法"bonferroni"、"BH"和"fdr"等。 在某些试验中,一个组有两个不同的因子控制,这时需要控制其中一个因子效应后比较另一个因子的效应。此时需要使用双因素 ANOVA。如果一个变量对结果的影响依赖于另一个变量的水平,那么这两个变量之间存在交互效应。 下面我们使用 R 自带数据集 ToothGrowth 进行说明,该数据集包括药物剂量和喂药方法两个变量。 进行双因素方差分析 由上述统计结果可以看出两个变量都对结果有显著的影响,下面将数据可视化展示。 如果想要进行任意两组之间的比较还可以使用下面几种方法: 如果不满足正态分布,则需要使用非参数检验** Kruskal-Wallis test**, 本文作者:思考问题的熊 版权声明:本博客所有文章除特别声明外,均采用 知识共享署名-非商业性使用-禁止演绎 4.0 国际许可协议 (CC BY-NC-ND 4.0) 进行许可。 如果你对这篇文章感兴趣,欢迎通过邮箱订阅我的 「熊言熊语」会员通讯,我将第一时间与你分享肿瘤生物医药领域最新行业研究进展和我的所思所学所想,点此链接即可进行免费订阅。写在前面
第六节 多样本均值分析
one-way ANOVA

library(ggpubr)
ggboxplot(PlantGrowth, x = "group", y = "weight",
color = "group", palette = c("#2072b8", "#ff6a38", "#1e993b"),
order = c("ctrl", "trt1", "trt2"),
xlab = "Treatment", ylab = "Weight" )
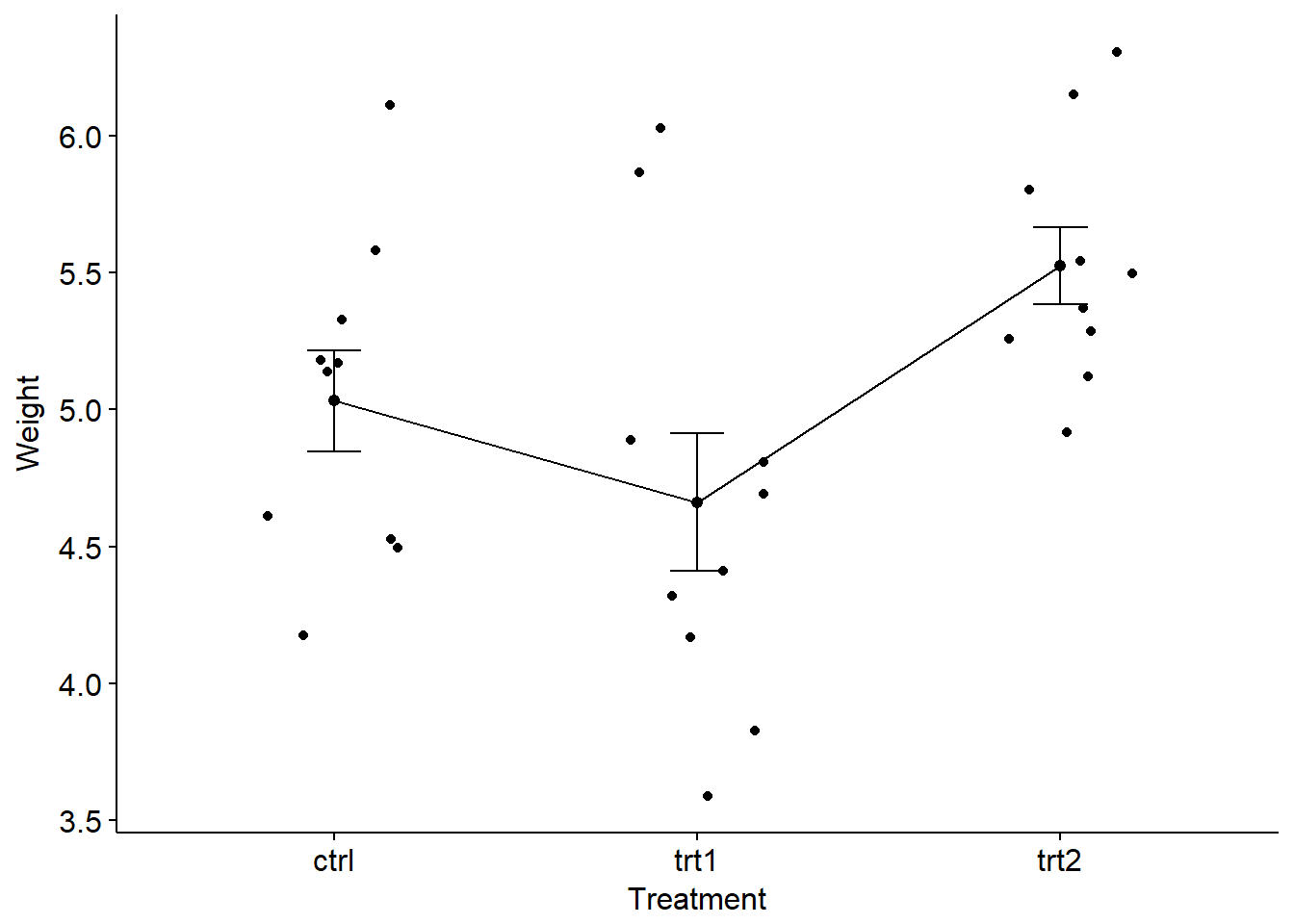
ggline(PlantGrowth, x = "group", y = "weight",
add = c("mean_se", "jitter"),
order = c("ctrl", "trt1", "trt2"),
ylab = "Weight", xlab = "Treatment")
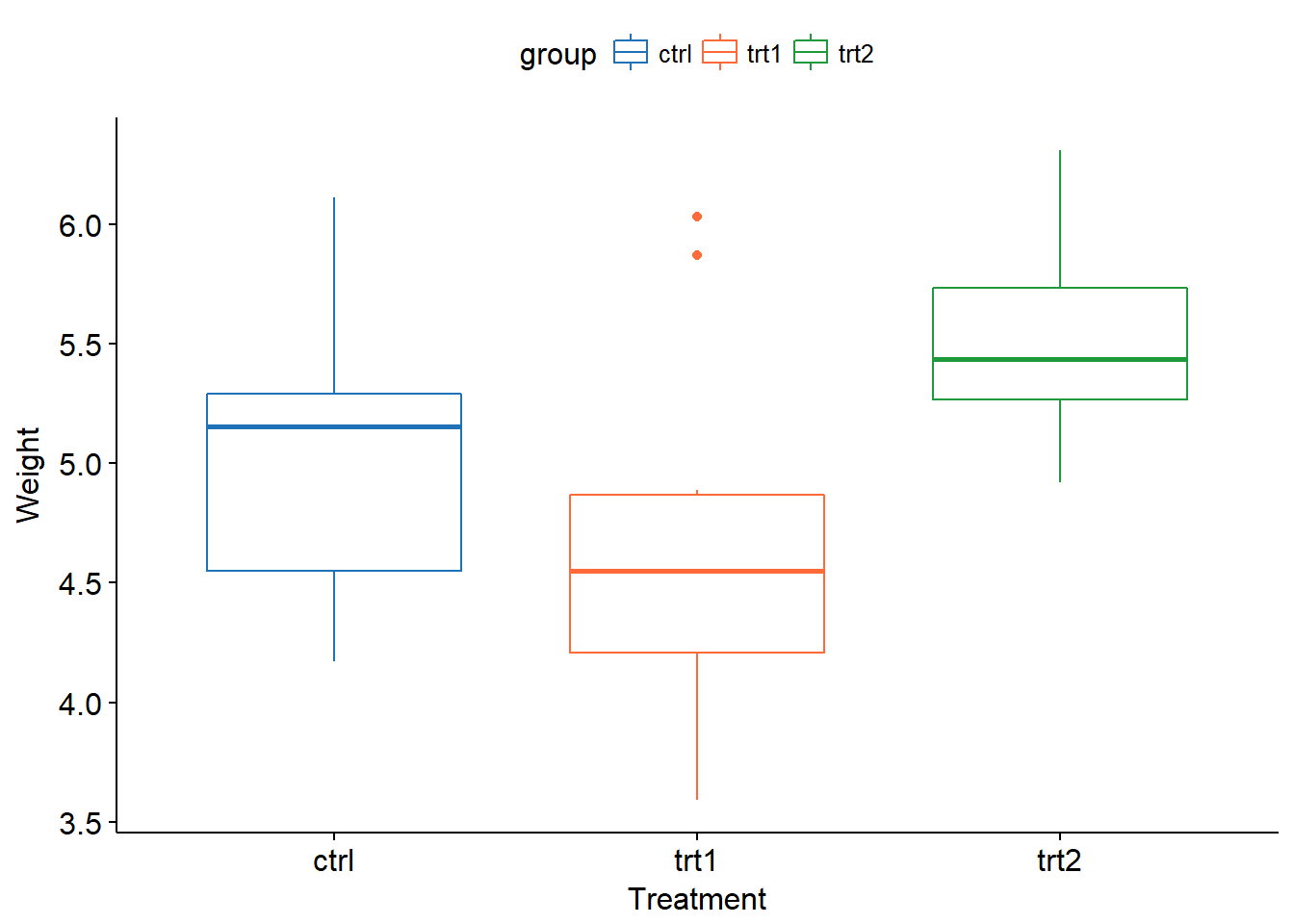
#检验方差齐性方法一
bartlett.test(weight ~ group, data=PlantGrowth)
#检验方差齐性方法二
library(car)
leveneTest(PlantGrowth$weight~PlantGrowth$group)
# Bartlett test of homogeneity of variances
#
# data: weight by group
# Bartlett's K-squared = 2.8786, df = 2, p-value = 0.2371
#
# Levene's Test for Homogeneity of Variance (center = median)
# Df F value Pr(>F)
# group 2 1.1192 0.3412
# 27
oneway.test();kruskal.test()和pairwise.wilcox.test()。pg.aov <- aov(weight ~ group, data = PlantGrowth)
summary(pg.aov)
# Df Sum Sq Mean Sq F value Pr(>F)
# group 2 3.766 1.8832 4.846 0.0159 *
# Residuals 27 10.492 0.3886
# ---
# Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
pairwise.t.test(PlantGrowth$weight, PlantGrowth$group,
p.adjust.method = "fdr")
# Pairwise comparisons using t tests with pooled SD
#
# data: PlantGrowth$weight and PlantGrowth$group
#
# ctrl trt1
# trt1 0.194 -
# trt2 0.132 0.013
#
# P value adjustment method: fdr
TukeyHSD(pg.aov)
# Tukey multiple comparisons of means
# 95% family-wise confidence level
#
# Fit: aov(formula = weight ~ group, data = PlantGrowth)
#
# $group
# diff lwr upr p adj
# trt1-ctrl -0.371 -1.0622161 0.3202161 0.3908711
# trt2-ctrl 0.494 -0.1972161 1.1852161 0.1979960
# trt2-trt1 0.865 0.1737839 1.5562161 0.0120064
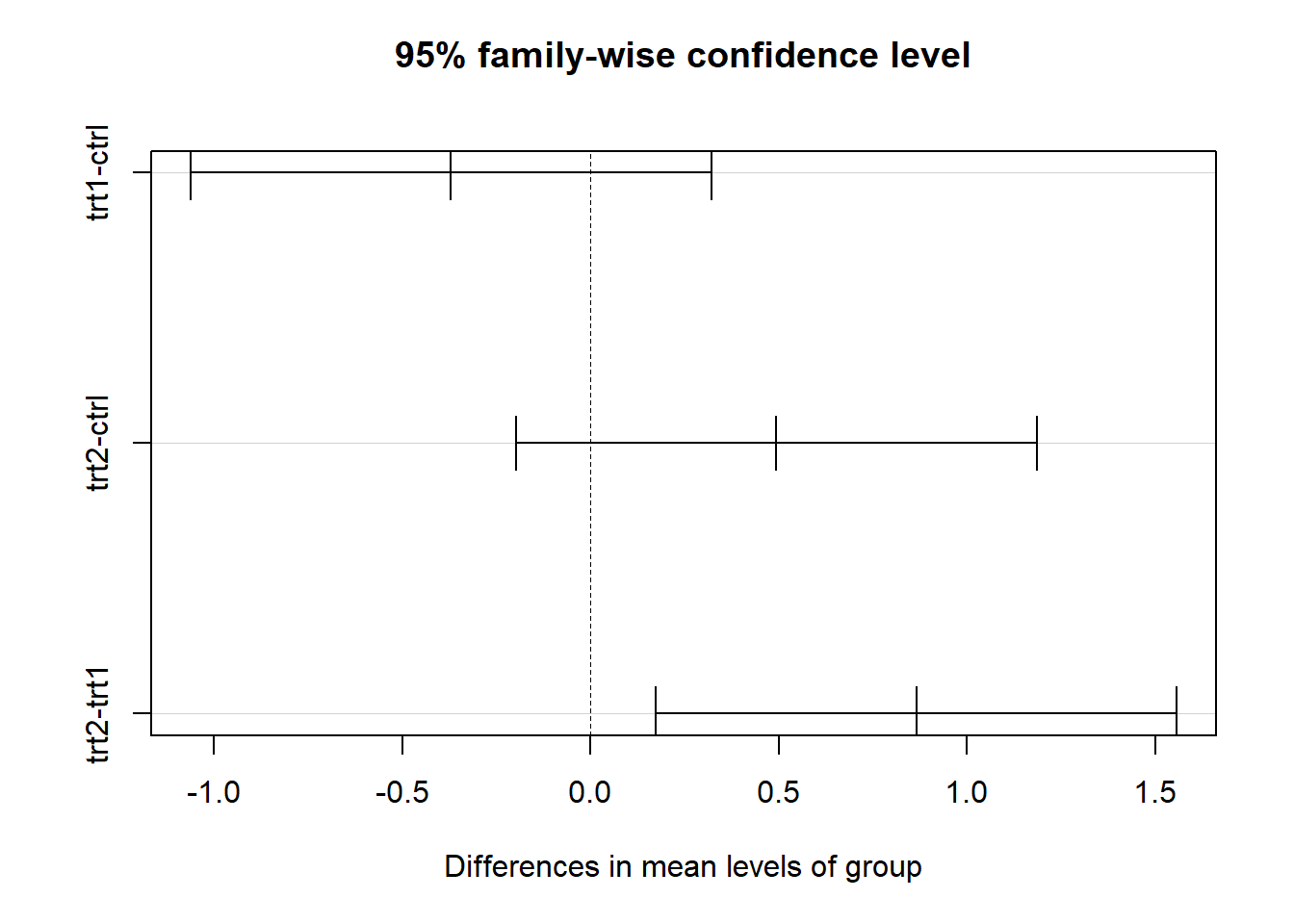
plot(TukeyHSD(pg.aov))
library(multcomp)
summary(glht(pg.aov, linfct=mcp(group="Dunnett")))
summary(glht(pg.aov, linfct=mcp(group="Tukey")))
# Simultaneous Tests for General Linear Hypotheses
#
# Multiple Comparisons of Means: Dunnett Contrasts
#
# Fit: aov(formula = weight ~ group, data = PlantGrowth)
#
# Linear Hypotheses:
# Estimate Std. Error t value Pr(>|t|)
# trt1 - ctrl == 0 -0.3710 0.2788 -1.331 0.323
# trt2 - ctrl == 0 0.4940 0.2788 1.772 0.153
# (Adjusted p values reported -- single-step method)
#
# Simultaneous Tests for General Linear Hypotheses
#
# Multiple Comparisons of Means: Tukey Contrasts
#
# Fit: aov(formula = weight ~ group, data = PlantGrowth)
#
# Linear Hypotheses:
# Estimate Std. Error t value Pr(>|t|)
# trt1 - ctrl == 0 -0.3710 0.2788 -1.331 0.391
# trt2 - ctrl == 0 0.4940 0.2788 1.772 0.198
# trt2 - trt1 == 0 0.8650 0.2788 3.103 0.012 *
# ---
# Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
# (Adjusted p values reported -- single-step method)
#
two-way ANOVA
# 检测不同条件样本量是否相等
table(ToothGrowth$supp,ToothGrowth$dose)
# 0.5 1 2
# OJ 10 10 10
# VC 10 10 10
summary(ToothGrowth)
# 发现 dose 并没有当做因子来处理,需要进行转换
# len supp dose
# Min. : 4.20 OJ:30 Min. :0.500
# 1st Qu.:13.07 VC:30 1st Qu.:0.500
# Median :19.25 Median :1.000
# Mean :18.81 Mean :1.167
# 3rd Qu.:25.27 3rd Qu.:2.000
# Max. :33.90 Max. :2.000
tg <- ToothGrowth
tg$dose <- factor(tg$dose, levels = c(0.5,1,2),
labels =c("low","mid","high") )
# 重新检查
summary(tg)
# len supp dose
# Min. : 4.20 OJ:30 low :20
# 1st Qu.:13.07 VC:30 mid :20
# Median :19.25 high:20
# Mean :18.81
# 3rd Qu.:25.27
# Max. :33.90
summary(tg.aov <- aov(tg$len~tg$supp*tg$dose))
## 正确做法
# Df Sum Sq Mean Sq F value Pr(>F)
# tg$supp 1 205.4 205.4 15.572 0.000231 ***
# tg$dose 2 2426.4 1213.2 92.000 < 2e-16 ***
# tg$supp:tg$dose 2 108.3 54.2 4.107 0.021860 *
# Residuals 54 712.1 13.2
# ---
# Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
summary(tmp.aov <- aov(ToothGrowth$len~ToothGrowth$supp*ToothGrowth$dose))
## 错误做法,不将 dose 转换为 factor,《R 语言实战》第一版用到这个例子的时候书上是错误的,第二版已经改正。
# Df Sum Sq Mean Sq F value Pr(>F)
# ToothGrowth$supp 1 205.4 205.4 12.317 0.000894 ***
# ToothGrowth$dose 1 2224.3 2224.3 133.415 < 2e-16 ***
# ToothGrowth$supp:ToothGrowth$dose 1 88.9 88.9 5.333 0.024631 *
# Residuals 56 933.6 16.7
# ---
# Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
library(ggplot2)
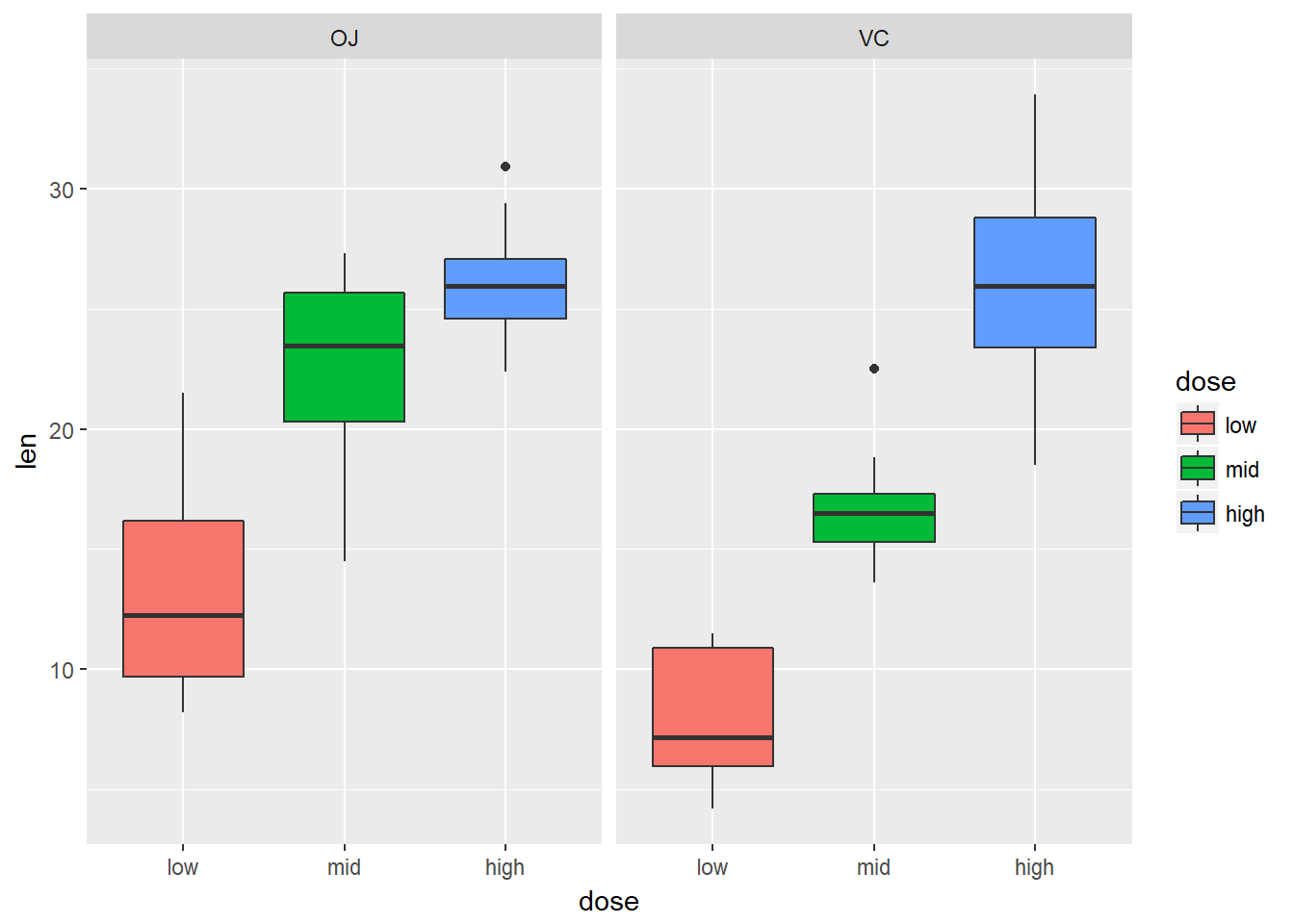
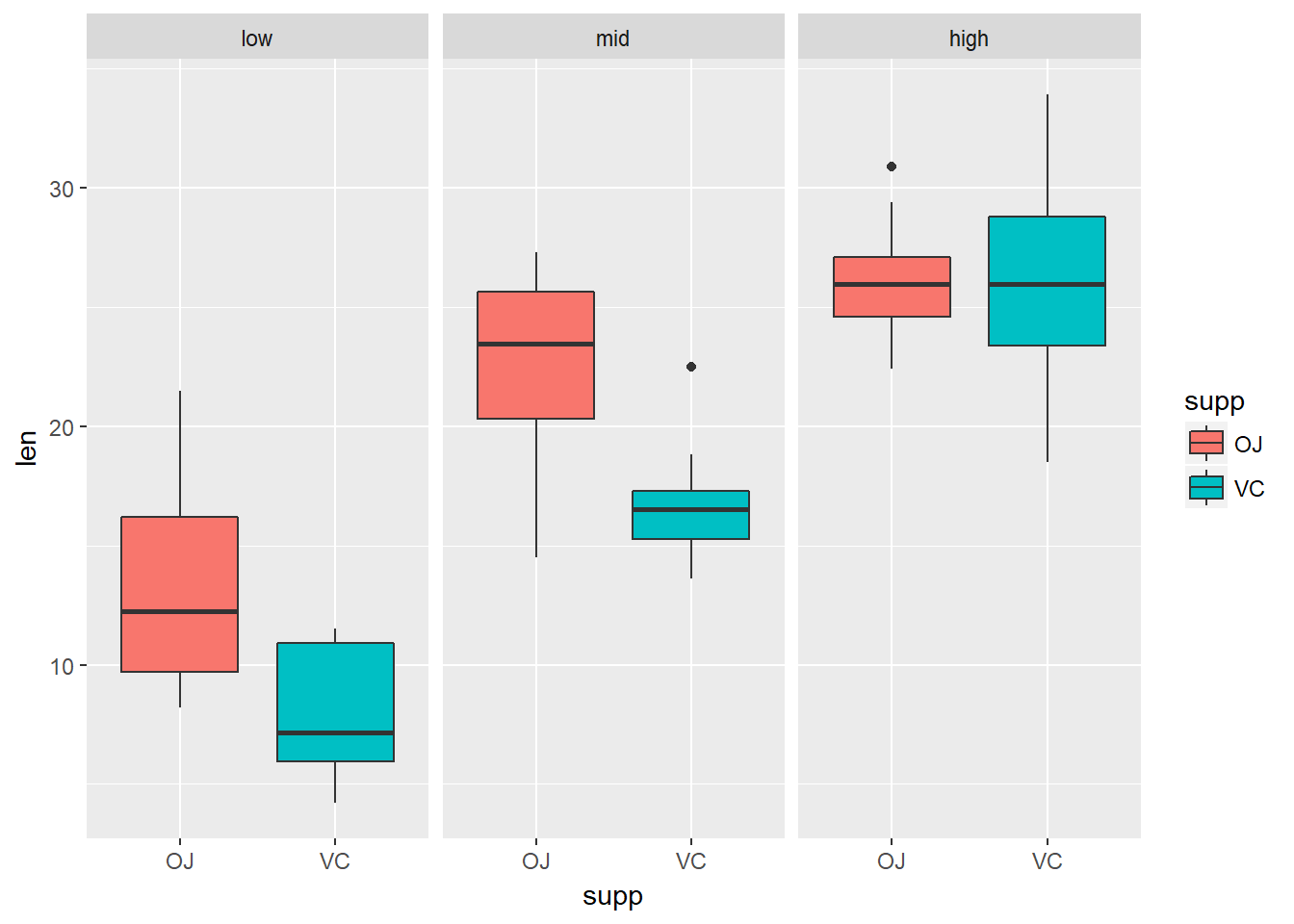
ggplot(tg, aes(x=dose,y=len))+geom_boxplot(aes(fill = dose))+facet_grid(.~supp)
ggplot(tg, aes(x=supp,y=len))+geom_boxplot(aes(fill = supp))+facet_grid(.~dose)
library(ggpubr)
ggboxplot(tg, x = "dose", y = "len", color = "supp",
palette = c("#2072b8", "#ff6a38"))
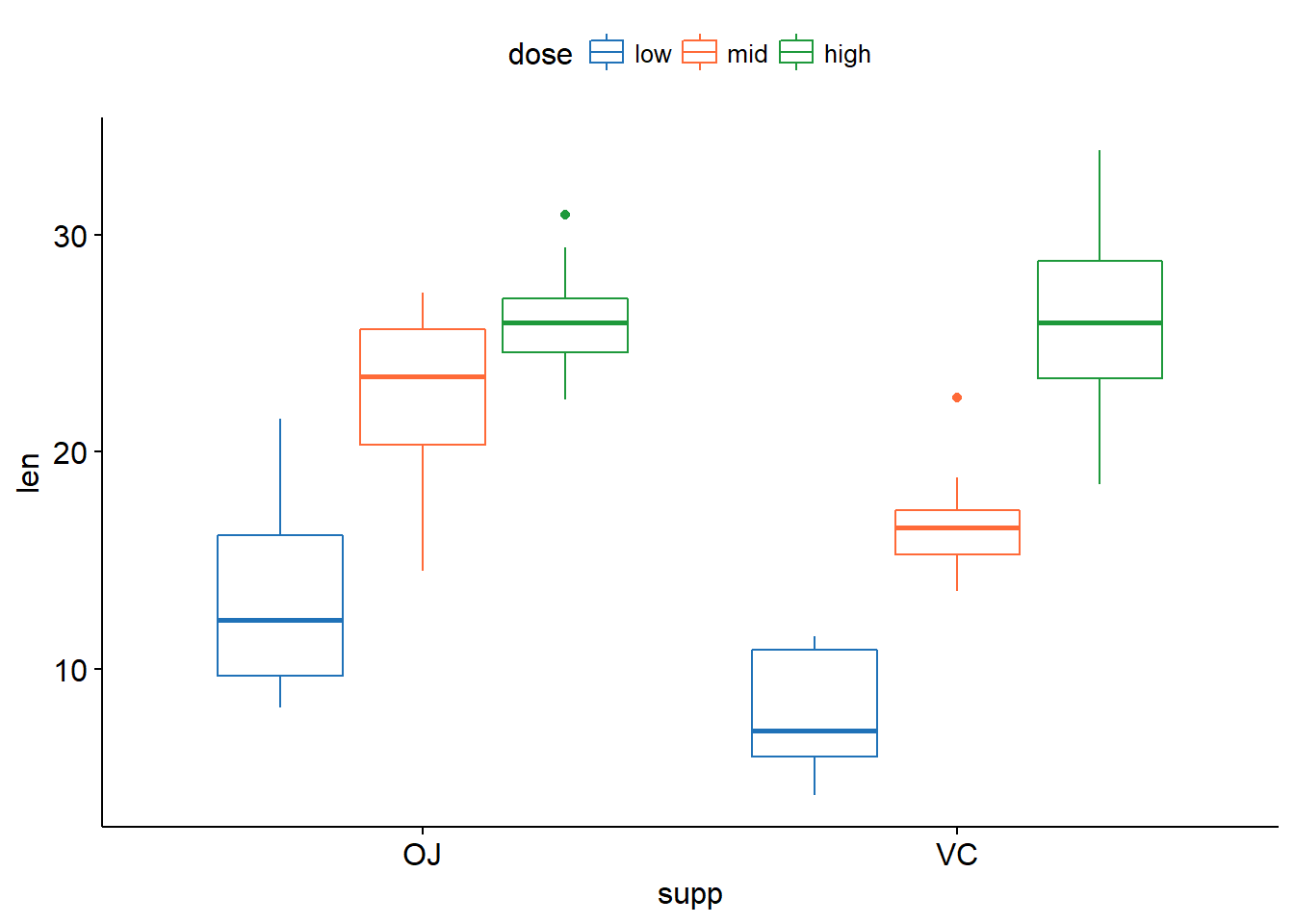
ggboxplot(tg, x = "supp", y = "len", color = "dose",
palette = c("#2072b8", "#ff6a38", "#1e993b"))
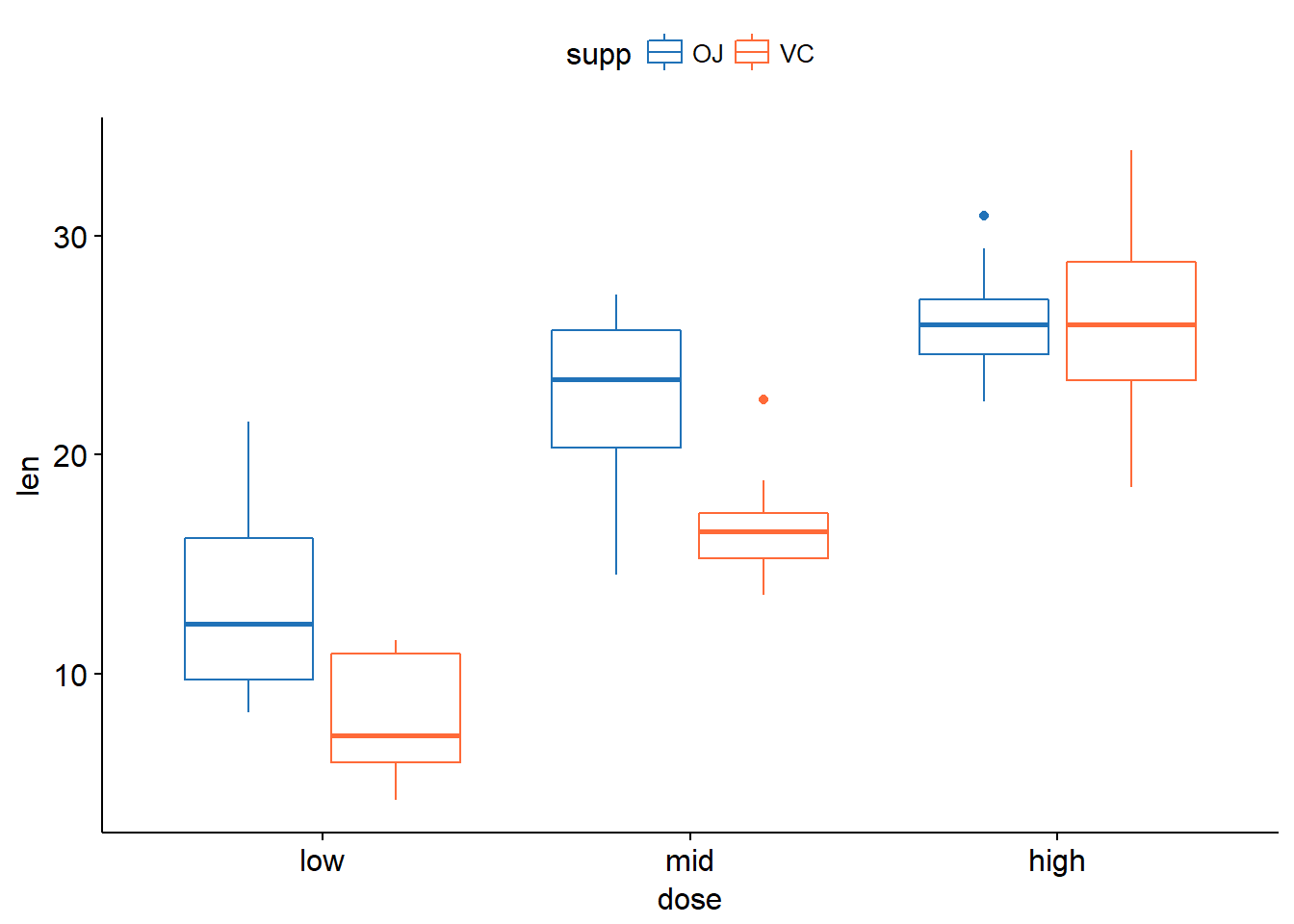
TukeyHSD(tg.aov)
# Tukey multiple comparisons of means
# 95% family-wise confidence level
#
# Fit: aov(formula = tg$len ~ tg$supp * tg$dose)
#
# $`tg$supp`
# diff lwr upr p adj
# VC-OJ -3.7 -5.579828 -1.820172 0.0002312
#
# $`tg$dose`
# diff lwr upr p adj
# mid-low 9.130 6.362488 11.897512 0.0e+00
# high-low 15.495 12.727488 18.262512 0.0e+00
# high-mid 6.365 3.597488 9.132512 2.7e-06
#
# $`tg$supp:tg$dose`
# diff lwr upr p adj
# VC:low-OJ:low -5.25 -10.048124 -0.4518762 0.0242521
# OJ:mid-OJ:low 9.47 4.671876 14.2681238 0.0000046
# VC:mid-OJ:low 3.54 -1.258124 8.3381238 0.2640208
# OJ:high-OJ:low 12.83 8.031876 17.6281238 0.0000000
# VC:high-OJ:low 12.91 8.111876 17.7081238 0.0000000
# OJ:mid-VC:low 14.72 9.921876 19.5181238 0.0000000
# VC:mid-VC:low 8.79 3.991876 13.5881238 0.0000210
# OJ:high-VC:low 18.08 13.281876 22.8781238 0.0000000
# VC:high-VC:low 18.16 13.361876 22.9581238 0.0000000
# VC:mid-OJ:mid -5.93 -10.728124 -1.1318762 0.0073930
# OJ:high-OJ:mid 3.36 -1.438124 8.1581238 0.3187361
# VC:high-OJ:mid 3.44 -1.358124 8.2381238 0.2936430
# OJ:high-VC:mid 9.29 4.491876 14.0881238 0.0000069
# VC:high-VC:mid 9.37 4.571876 14.1681238 0.0000058
# VC:high-OJ:high 0.08 -4.718124 4.8781238 1.0000000
#上述结果如果感觉过于复杂,可以使用下面下面的形式
TukeyHSD(tg.aov,which = "tg$dose")
# Tukey multiple comparisons of means
# 95% family-wise confidence level
#
# Fit: aov(formula = tg$len ~ tg$supp * tg$dose)
#
# $`tg$dose`
# diff lwr upr p adj
# mid-low 9.130 6.362488 11.897512 0.0e+00
# high-low 15.495 12.727488 18.262512 0.0e+00
# high-mid 6.365 3.597488 9.132512 2.7e-06
# 或者
pairwise.t.test(tg$len,tg$dose)
# Pairwise comparisons using t tests with pooled SD
#
# data: tg$len and tg$dose
#
# low mid
# mid 1.3e-08 -
# high 4.4e-16 1.4e-05
#
# P value adjustment method: holm
kruskal.test()和pairwise.wilcox.test()。
· 分享链接 https://kaopubear.top/blog/2017-10-01-RandStatistics6/