入门生物信息,所有人都绕不开统计基础知识和相关实现方式。本章我们将简要介绍统计学相关基础知识以及如何使用 R 语言进行简单地计算和分析。 本节提到的相关性分析和后面会提到的 t-test, ANOVA 以及回归分析等被称为参数检验,这些检验在进行时我们常默认数据符合一定前提条件,如符合正态分布和方差相等等。当样本数量大于 30 时,根据中心极限定理,我们通常认为数据符合正态分布;在进行 t-test 和 ANOVA 分析时,还需要满足样本方差相等。 在进行各种检验之前需要初步检验数据是否符合某种检验的前提条件,如果不符合则应该考虑使用非参数检验或其他方法。 在评估数据集是否符合正态分布时通常会采用** Shapiro-Wilk’s test 和图示 (Q-Q plot) **结合的方法。使用 Q-Q plot(quantile-quantile plot) 的结果较直观,使用 Shapiro-Wilk’s test 显著性检验的方法更准确(相对而言)。 Shapiro-Wilk’s test 结果受样本量的影响非常大,当样本量很大时即便数据符合正态分布也容易出现 p 值很小进而拒绝原假设的情况(该检验原假设是样本来自于正态分布)。样本量很小时即便真实数据不 s 是来自正态分布,也可能接受原假设。 这里试举一例 可以发现,即便我们生成的两个样本都不是正态分布,但是检验的结果仍然没有拒绝原假设(没有拒绝不等于接受原假设)。好在 R 中该函数限制检测的样本个数是 3 到 5000。因此,同时结合图像来分析还是很必要的。 一般使用 Q-Q plot 来检验是否符合正态分布,R 中默认的函数是 下面利用生成的数据绘图。 **Pearson **相关系数、**Spearman **相关系数、**Kendall **相关系数都可以用来表示变量之间的相关性,一般情况使用 pearson 相关系数更多,如果明确样本不符合正态分布可以使用 kendall 或者 spearman 相关系数。这三种相关系数都可以通过 pearson 相关系数计算公式
其中 m 表示均值。 可以使用散点图进行两个变量之间的相关性展示。 前面我们只是计算了两个变量之间的相关性,还应该对相关进行显著性检验。原假设为变量之间没有相关性,使用函数为 统计结果中,t 表示 t 检验统计量,df 表示自由度,pvalue 是 t 检验的显著性水平,conf.int 表示 95%的置信区间,sample estimates 是相关系数。相关系数越接近-1 表示负相关,接近 1 表示正相关。 本文作者:思考问题的熊 版权声明:本博客所有文章除特别声明外,均采用 知识共享署名-非商业性使用-禁止演绎 4.0 国际许可协议 (CC BY-NC-ND 4.0) 进行许可。 如果你对这篇文章感兴趣,欢迎通过邮箱订阅我的 「熊言熊语」会员通讯,我将第一时间与你分享肿瘤生物医药领域最新行业研究进展和我的所思所学所想,点此链接即可进行免费订阅。写在前面
第四节 相关性分析
正态分布评估
# 分别随机生成两组二项分布和指数分布随机数
set.seed(90)
x <- rbinom(15,8,0.7)
y <- rexp(15,0.5)
shapiro.test(x)
shapiro.test(y)
# Shapiro-Wilk normality test
#
# data: x
# W = 0.95996, p-value = 0.6917
#
# Shapiro-Wilk normality test
#
# data: y
# W = 0.96168, p-value = 0.7216
qqnorm();ggplot2 中可以使用函数qplot();qqpubr 包是基于 ggplot2 二次开发的简易升级版,操作更加友好,可以使用函数ggqqplot()。# 生成符合正态分布的一组数据并绘图
z <- rnorm(50)
qqnorm(z)
library(ggplot2)
qplot(sample=z)
library(ggpubr)
ggqqplot(z)
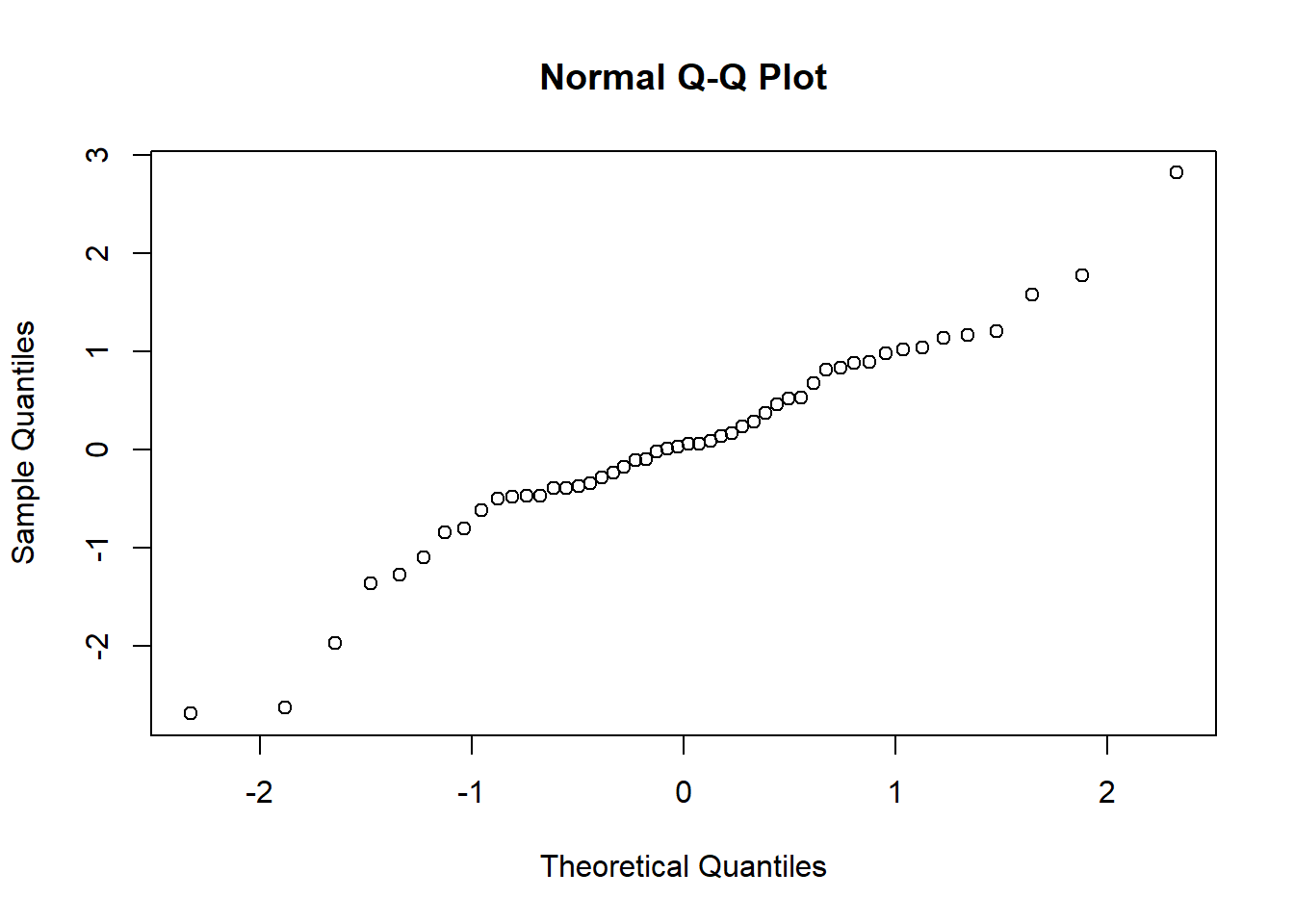
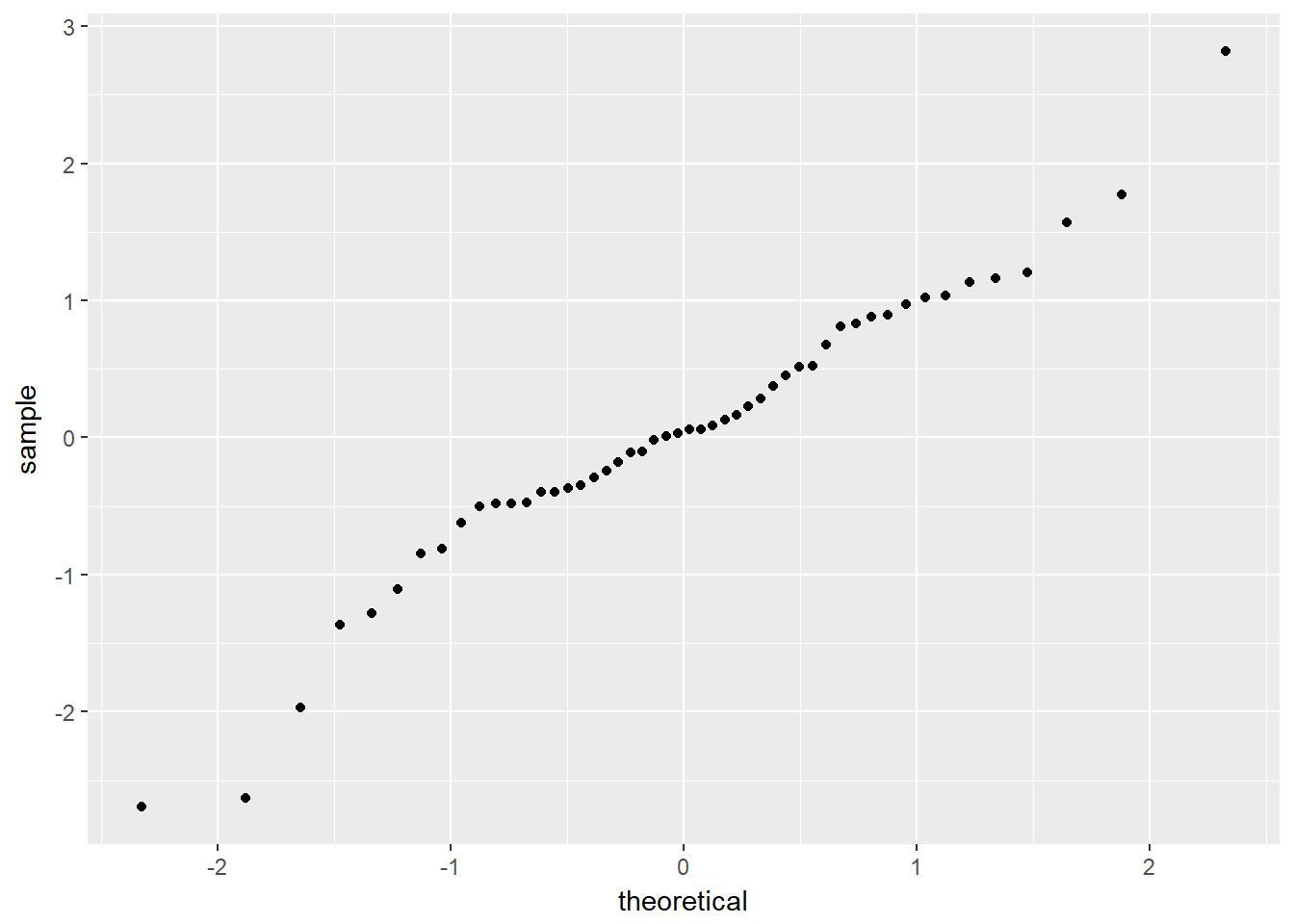
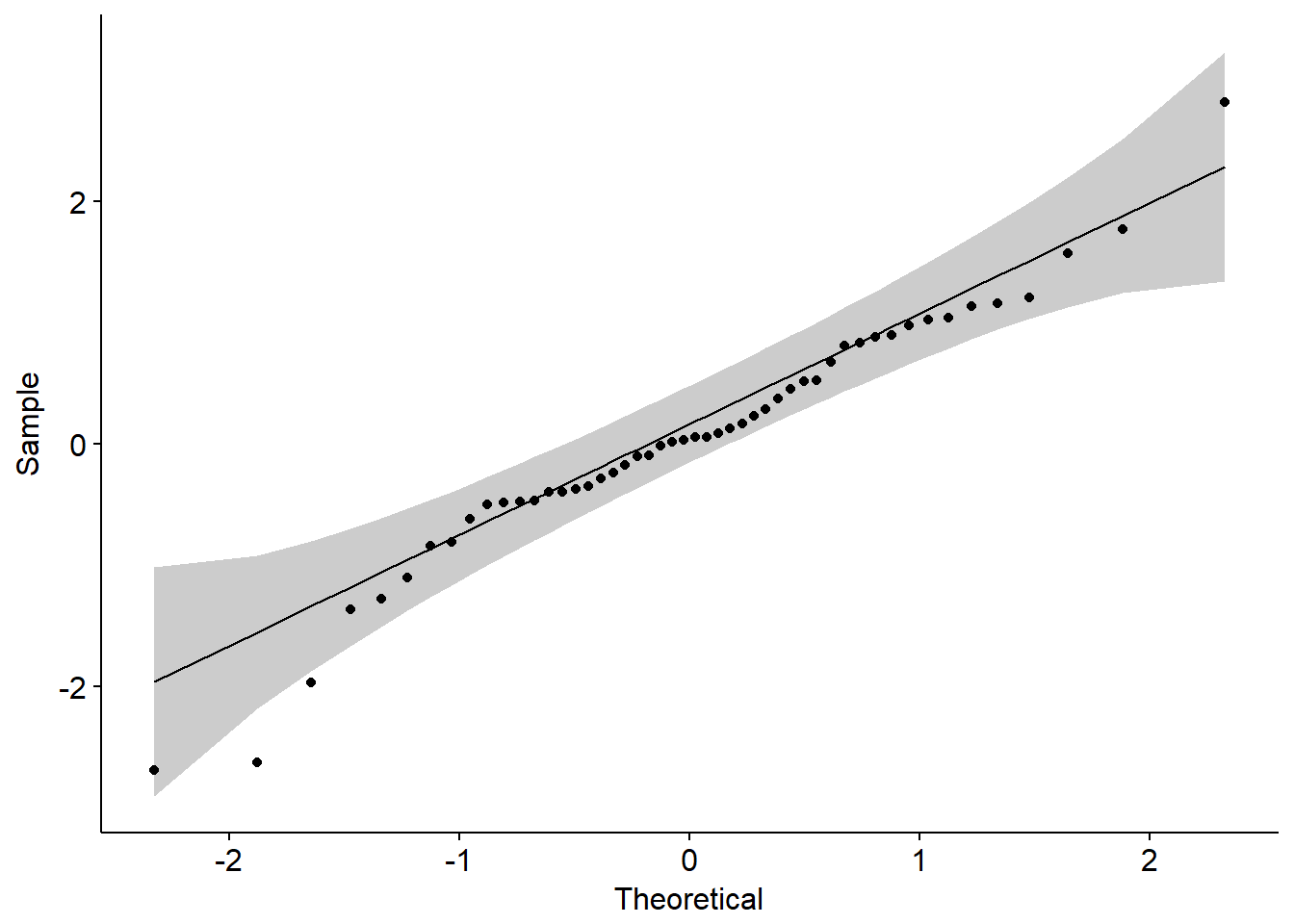
相关性分析
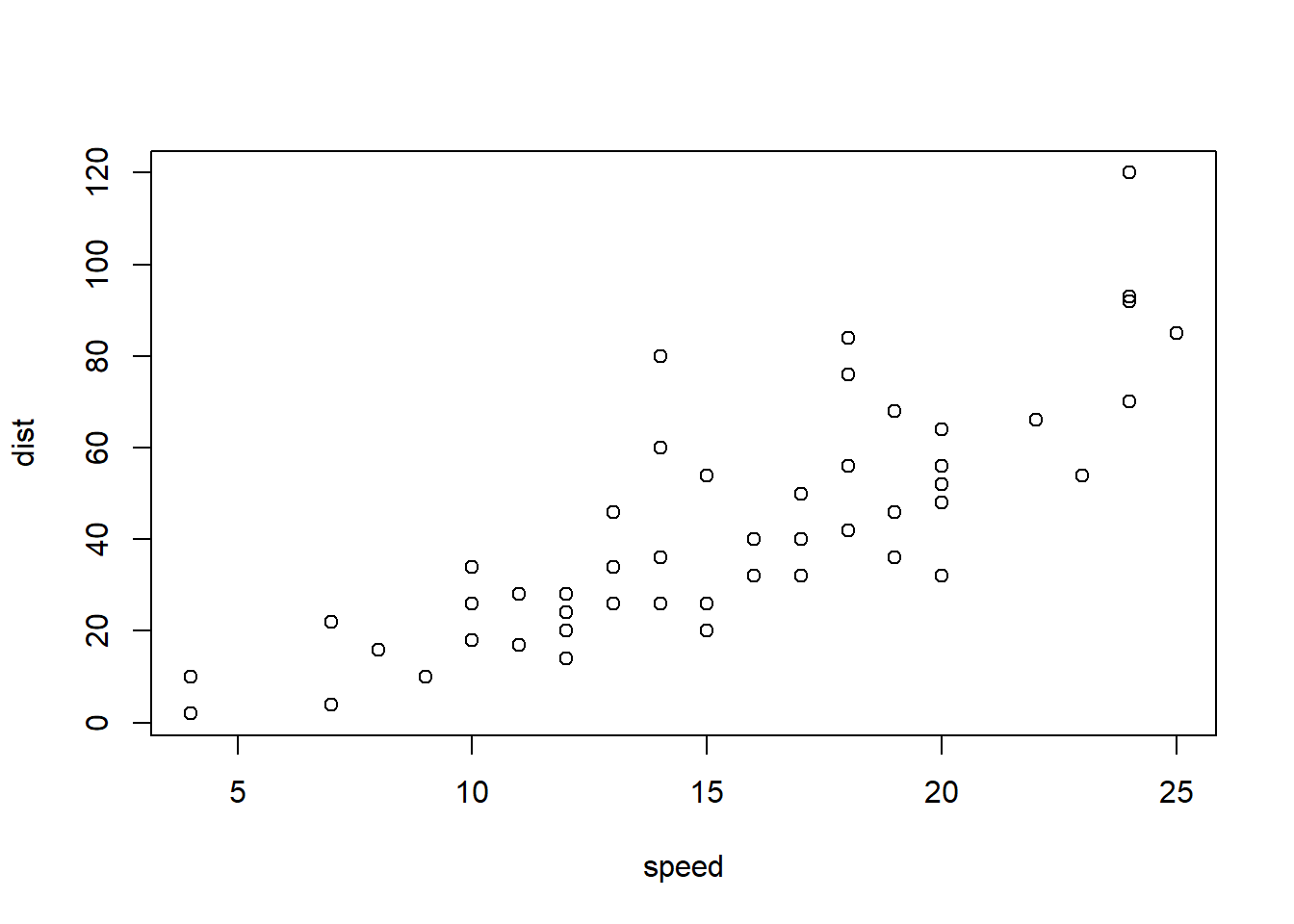
cor()函数来进行计算,下面通过 R 已有数据集 cars,查看汽车车速和刹车距离之间的相关性。cor(cars, method = "pearson")
相关性可视化展示
plot(cars)
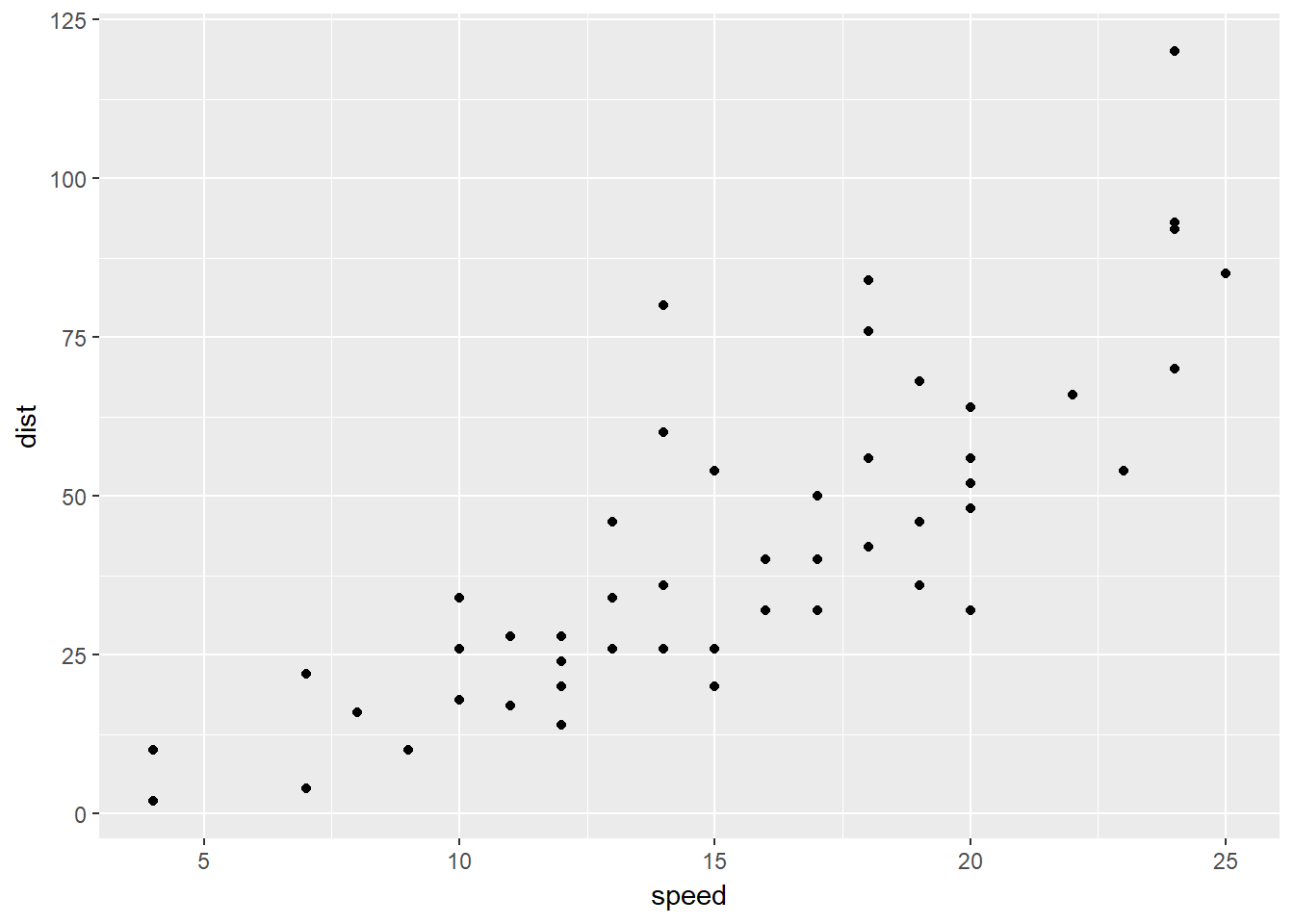
ggplot(cars, aes(x=speed, y=dist))+ geom_point()
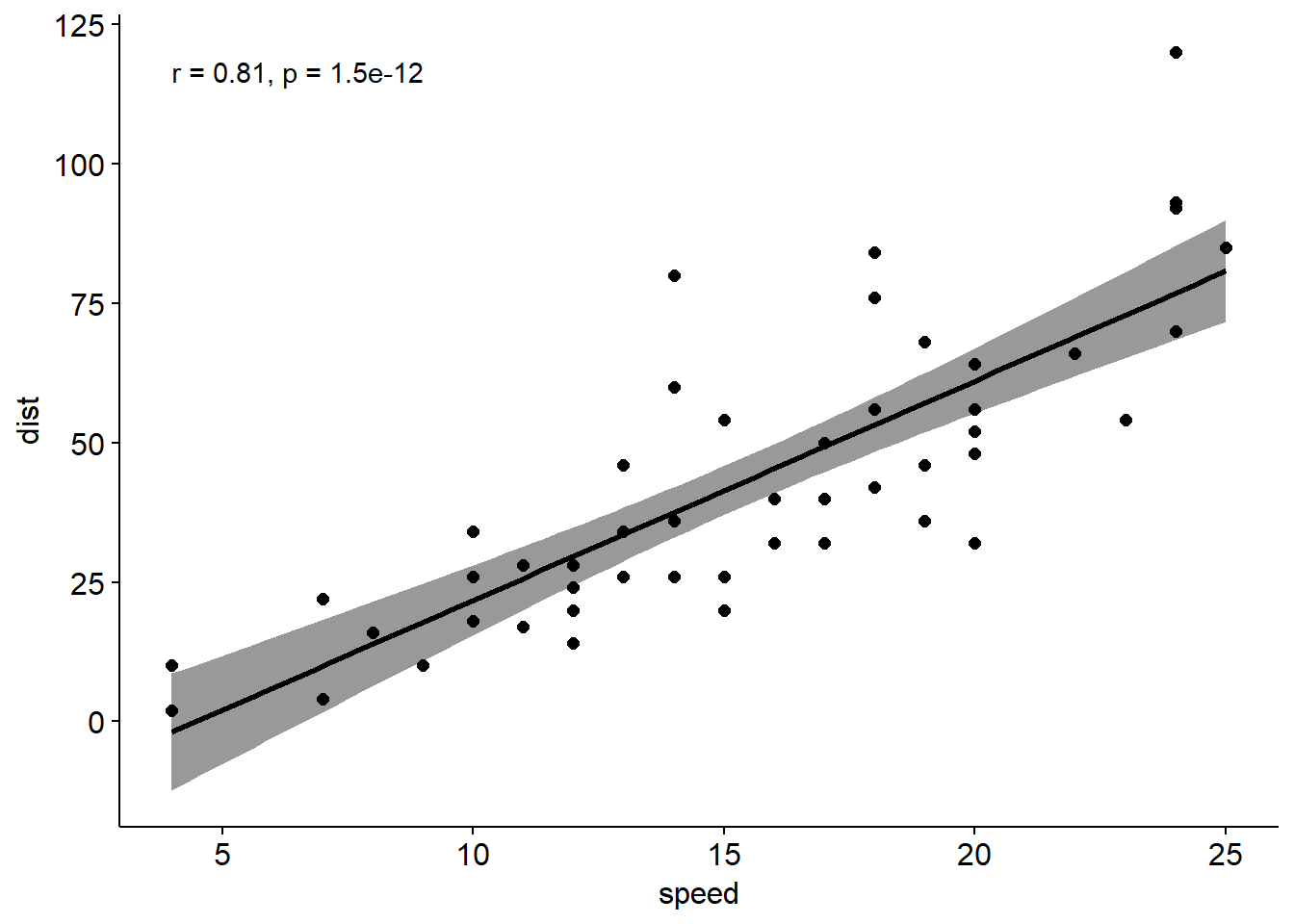
ggscatter(cars,x="speed", y="dist",\
add = "reg.line", conf.int = T,cor.coef = T)
Pearson 相关性检验
cor.test()cor.test(cars$speed,cars$dist,\
alternative = "two.side", method = "pearson")
· 分享链接 https://kaopubear.top/blog/2017-09-28-RandStatistics4/